Parameters

I said previously that the theory of chemistry kind of doesn’t have any free parameters. Here’s a more detailed explanation of what I mean by that. Also, this is another difference between 3D and 4D chemistry, since in 4D, there are parameters.

Let’s start, as usual, with Schrödinger’s equation (for a 3D atom), in this case with all of the constants included explicitly, since those are what we’re discussing.

$i \hbar \frac {\mathrm d}{\mathrm dt} \psi = - \frac {\hbar ^2}{2m} \nabla^2 \psi - \frac {Ze^2}{4 \pi \epsilon_0 r} \psi$

The constants involved are

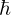$\hbar$ , reduced Planck’s constant
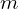$m$ , the electron mass (or, to be more precise, the reduced mass of the system)
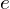$e$ , the electron charge
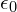$\epsilon_0$ , the permittivity of the vacuum

where the nuclear charge is assumed to be some integer multiple $-Z$ of the electron charge (exploring what happens when nuclear charge is allowed to vary continuously could also be interesting, but like the change to 4D, that feels more like changing the rules entirely than tweaking a parameter).

In order to get rid of the constants, we need to change the units we’re using so that the values of $\hbar$ , $m$ , $e$ and $\frac 1 {4 \pi \epsilon_0}$ , as expressed in those units, become 1. (The charge $e$ could be ignored if we just set $\frac {e^2}{4 \pi \epsilon_0}$ as a whole to 1, but if we want a unit of charge it may as well be $e$ .) The following units are suitable

For energy, 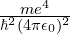$\frac{m e^4}{\hbar^2 (4 \pi \epsilon_0)^2}$ , AKA the Hartree
For length, $\frac{\hbar^2 4 \pi \epsilon_0}{me^2}$
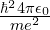
For time, $\frac{\hbar^3 (4 \pi \epsilon_0)^2}{m e^4}$
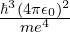
And for charge, simply $e$ .

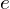These are known as atomic units. Expressed in these units, Schrödinger’s equation for a single atom becomes

$i \frac {\mathrm d}{\mathrm dt} \psi = - \frac 1 2 \nabla^2 \psi - \frac Z r \psi$

(it would be possible to also eliminate the factor of $\frac 1 2$ in the kinetic term, but it is conventional not to.)

If those four constants changed, it might therefore affect the overall size or energy of atoms, but the fundamental behaviour would remain the same. There would still be the same elements, molecules and reactions. There are other parameters that could lead to some slight differences if changed though.

For one, the equation given describes only the dynamics of the electrons, not the nuclei. With the electron mass fixed at 1, the nuclear masses are genuine free parameters. On a fundamental level, they’re determined by the proton-electron mass ratio and the ratios of the masses of the different nuclei are fixed, but from the point of view of chemistry, they’re just parameters to be taken as input.

The nuclei are so much more massive and slow-moving than the electrons that their masses don’t have much influence on most basic chemical properties, like which molecules are stable. At a higher level though, they do matter. Most obviously, the mass of a compound as a whole is almost entirely the mass of its nuclei. Molecular vibrations determine some of the lower-frequency parts of the absorbtion spectrum, and determine thermal properties like heat capacity and thermal conductivity. Lattice vibrations in metals interact with the free electrons and are one of the main limiting factors of the metals’ electrical conductivity conductivity. Chemical reactions depend on nuclei moving of course, so their rates are affected. I’m not sure whether melting and boiling points would be affected much. The melting point of deuterium differs significantly from that of hydrogen-1, but there is a theoretical argument why there should not be much difference in general (the enthalpy of vaporisation is not affected much, and the entropy of vaporisation is presumably mostly determined by the entropy of the gas phase, which is also not affected much), so the case of hydrogen might just be because its nucleus is light enough that it has an unusually significant effect on the chemistry.

If nuclei were much lighter, closer in mass to the electron, this would make their masses much more important, but it would also make everything more complicated. Often in chemistry it is possible to treat the nuclei like classical particles, and in simulating the electrons it is common to use the approximation that the nuclei are entirely static (the Born-Oppenheimer approximation), which makes the simulations much easier. If the nuclei were much lighter, this would not be possible. I would guess that if the nuclei were much lighter, there would be less of a tendency for molecules to have distinct shapes and bond structures.

The other minor free parameter is the speed of light, or equivalently the fine-structure constant (in atomic units, the speed of light is the reciprocal of the fine structure constant). It does not appear in Schrödinger’s equation because that is a non-relativistic approximation. It is related to the relative strengths of electric and magnetic forces, but it also affects things like spin-orbit coupling, and when electrons (or anything else) are travelling at large fractions of the speed of light, they act a bit like they have more mass. In atomic units, $c \approx 137$ , and the electrons’ typical speeds go up to around $Z$ . For light elements with atomic numbers much smaller than 137, relativistic effects are therefore not very important, but the atomic numbers of the known elements go up to 118 (at least for now), and the atomic numbers of the elements it’s practical to collect macroscopic quantities of and perform experiments on go up to around 100, so for heavy elements the value of $c$ can become significant. If it were lower, there would presumably be even more peculiar effects along the lines of those predicted for superheavy elements. If the fine structure constant were sufficiently high (I assume somewhere near 1), quantum electrodynamics would begin to break down entirely as the Landau pole became increasingly relevant to low-energy scenarios. (A very simplified calculation would give the total energy of positronium (an electron bound to a positron), including the rest masses of its constituents, as negative. More accurate calculations would give diverging sums.)

There are even more minor contributions from other things like the internal structure of the nucleus, the weak force (which affects electrons, but is very weak as its name suggests) and virtual particles of other types, but all of them are negligible unless you try really hard to go looking for them, and they’re more physics than chemistry anyway.

Going back to major effects, let’s consider Schrödinger’s equation for a 4D atom.

$i \hbar \frac {\mathrm d}{\mathrm dt} \psi = - \frac {\hbar ^2}{2m} \nabla^2 \psi - \frac {Ze^2}{2 \pi^2 \epsilon_0 r^2} \psi + \frac {Zk_s \exp(-lr)}{r^2} \psi$

There are now two new parameters relating to the s-force. $l$ , which determines its length scale and relates to the mass of the associated force-carrying boson, and $k_s$ , which combines the charge (like $e$ ) and interaction strength (like $\epsilon_0$ ).

Because the Coulumb term changed from being proportional to $\frac 1 r$ to $\frac 1 {r^2}$ , the factor $\frac{e^2}{2 \pi^2 \epsilon_0}$ now has dimensions $\text{energy} \times \text{length}^2$ , which is the same as $\frac {\hbar^2} m$ , so they can’t be used to determine a length or energy scale like in the 3D case. The ratio between them is a dimensionless constant, so it cannot be removed just by changing the units. This is related to the fact that the dynamics without the additional s-force term is scale invariant. Instead, the constant $\frac 1 l$ can be used as the unit of length, then $\frac {\hbar^2 l^2}{m}$ is the unit of energy and that divided by $\hbar$ is the unit of time.

With these units, the equation becomes

$i \frac {\mathrm d}{\mathrm dt} \psi = - \frac 1 2 \nabla^2 \psi - \frac {Ze^2}{2 \pi^2 \epsilon_0 r^2} \psi + \frac {Zk_s \exp(-r)}{r^2} \psi$

To make this look neater, let’s define the constant $k_e = \frac{e^2}{2 \pi^2 \epsilon_0}$ , then it becomes

$i \frac {\mathrm d}{\mathrm dt} \psi = - \frac 1 2 \nabla^2 \psi - Z\frac {k_e - k_s \exp(-r)}{r^2} \psi$

The constants $k_e$ and $k_s$ are genuine parameters whose values significantly affect how this model of chemistry behaves. Also, I’ve assumed that the nuclear s-charge is proportional to the atomic number, but this doesn’t actually need to be the case. If the nuclei are composed of a variable ratio of protons and neutrons like in real life, there’s no reason the charge of the neutron would have to be $0$ just because its electric charge is. If the neutron has a non-zero s-charge, nuclei with the same number of protons and different numbers of neutrons would end up behaving like completely different elements, to the point where it hardly seems to make sense calling them isotopes. Most of my previous simulations have assumed a fixed ratio of $k_e$ to $k_s$ , but relaxing this restriction could give more room to find a range of interesting elements all within the same model.

One particularly neat possibility is to have $k_e = k_s$ . If this is the case, the total potential becomes $Zk_e \frac{1-\exp(-r)}{r^2}$ , which for small $r$ is approximately equal to $\frac {Zk_e} r$ , so the total force on the electron would behave like an inverse-square law attraction at short ranges and inverse-cube law at long ranges. The force between the electrons would still be inverse-cube though, so this would still not be entirely similar to the 3D case. I find this option a little unsatisfying, since it feels like it’s going too far towards fighting the implications of 4D rather than accepting and exploring them. Also some of my programs can’t deal with it because they assume the wavefunction takes the sort of shape you get for $k_s > k_e$ . The case $k_s < k_e$ is just as degenerate as $k_s = 0$ with the electrons still collapsing into the nucleus, so I will not be considering it. Another neat possibility would be to assume that the s-charge of the neutron is equal to the electric charge of the proton. If the proton also has the same s-charge, this would give a ratio $k_s \approx 2k_e$ for most elements, or if the proton has no s-charge, it would imply $k_s \approx k_e$ in most cases, with hydrogen-1 being degenerate and isotopes being especially different from each other.

The lower $k_e$ is, the more chance the electrons will not be bound at all, and the higher $k_e$ is, the more tendency there is for all of the shells to collapse into one, and in between the two extremes, there is a regime that looks a little like real chemistry, but in no case is there an orderly periodic table like in 3D. I may explore the differences that changing the two parameters makes in more detail in some future post.

The nuclear masses and fine structure constant still exist, but the fine structure constant is less important than in real life. Because of the s-force’s region of repulsion, the place with the most electron density is not at the nucleus, but in a shell near $r=1$ . This gets slightly closer in as the atomic number increases, but not by very much. This means that at no point do the electrons end up travelling extremely fast, so any large-ish value of the speed of light will be irrelevant for anything except magnetism and optics. This is rather convenient, since relativistic simulations are harder and it’s nice to have an excuse to not use them.

Comments

Leave a Reply Cancel reply