Diffusion Monte-Carlo

Diffusion Monte-Carlo is one approach to actually calculating the results of the Schrödinger Equation. It isn’t used as extensively as some other methods because of its significant issues with high computational cost, but I’m starting my discussion of actual simulation techniques with it because it requires fewer approximations than other more efficient methods, and is in some ways conceptually simpler.

Derivation

To understand a system, we first try to find its ground state, the solution to the time-invariant Schrödinger Equation with the lowest energy. The equation we start with is $E\Psi = -\frac 1 {2m} \nabla^2 \Psi + V \Psi$ , which can be abbreviated $E\Psi = H\Psi$ where $H = -\frac 1 {2m} \nabla^2 + V$ (this doe not just trivially reduce to $E = H$ because $H$ is a linear operator, not a number, so $H\Psi$ is actually the function $H$ applied to $\Psi$ , not a product).

Any initial guess $\Psi_0$ (it doesn’t have to be a good guess at all, just so long as it isn’t exactly orthogonal to the ground state) can be expressed as a linear combination of states of definite energy $\Psi_0 = \sum_i a_i \psi_i$ , where $E_i \psi_i = H \psi_i$ (there are a lot of caveats to this, but I will continue to treat this simple version as true). Applying $H$ gives $H\Psi_0 = \sum_i a_i E_i \psi_i$ , which has a larger proportional contribution from the state of largest negative energy, the ground state, and is therefore a better approximation to the ground state provided all of the $E_i$ s are negative, but usually there will also be even bigger contributions with large positive $E_i$ too so this on its own is not satisfactory. Instead, take $\Psi_t = e^{-tH}\Psi_0 = \sum_i a_i e^{-tE_i} \psi_i$ . The largest contributions now come from the states of lowest energy, with the ground state being increasingly dominant as $t$ increases. The exponential $e^{-tH}$ here is defined by its power series $\sum_{n=0}^\infty \frac{(-tH)^n}{n!}$ .

This $\Psi_t$ can be calculated iteratively using the differential equation $\frac {\mathrm d}{\mathrm dt} \Psi_t = -H \Psi_t = \frac 1 {2m} \nabla^2 \Psi_t - V \Psi_t$ . This is similar to the time-depentent Schrödinger Equation, but with the derivative being different by a factor of $i$ , so instead of states changing phase at a rate proportional to their energy, they change in magnitude and, after appropriate re-scaling, $\Psi_t$ tends towards the ground state. Since it is equivalent to the Schrödinger Equation with time multiplied by $i$ , it is called the Imaginary-Time Schrödinger Equation

The equation is still impractical to solve explicitly, and by adding the variable $t$ it has only become more complicated than the original, but it now takes the form of a diffusion equation. If a particle is moving randomly (undergoing brownian motion), the probability density to find it at a point $x$ at a time $t$ is governed by the equation $\frac {\mathrm d}{\mathrm dt} p(x,t) = a \nabla_x^2 p(x,t)$ (where $a$ is a parameter that determines how fast it moves). It’s the same equation governing the flow of heat and dissolved chemicals (provided the medium isn’t moving). Since it describes randomly moving particles, it is also possible to go in the other direction, to simulate random motion of a large number of particles and use their distribution to approximate the solution to the diffusion equation. The $V$ term which is present in the Imaginary-Time Schrödinger Equation but not the diffusion equation has the effect of increasing the value of the wavefunction/probability density proportionally to its current value in areas where $V$ is low, and decreasing it in areas where $V$ is high, which can be included in the simulation by having the particles duplicate or delete themselves rather than just moving.

These particles are not the physical particles in the system (electrons, nuclei, etc.). Each of them moves in $nd$ -dimensional space, where $n$ is the number of physical particles and $d$ is the number of physical dimensions, and the position corresponds to one possible position of all of the physical particles at once.

With the method as stated, the number of particles increases exponentially like $e^{-tE_0}$ where $E_0$ is the ground-state energy. To prevent this, the potential is offset by $E_0$ , which shifts the ground-state energy to $0$ , but $E_0$ is one of the things that the simulation is meant to calculate, so this is done iteratively to keep the number of particles stable. The rate of growth is measured, giving an approximation of the ground state energy, which can then be used as feedback to keep the average rate of growth at $0$ .

In addition to the energy, some other properties of the molecule, such as its geometry, dipole moment, polarizability, and the strength of the London dispersion force between two molecules, can also be calculated. The method follows from the fact that these properties can be expressed as the derivative or second derivative of the energy with respect to some perturbation in the potential. This mostly doesn’t seem to have worked very well when I tried to implement it, but possibly there was just too much noise for the results to be clear.

Limitations

Most obviously, this method uses random values and produces correct results only on average. The variance can be quite high, and additional complications are usually required to get sufficiently precise answers. In theory though, it is sufficient to just average the results over a very long run-time to get answers to any desired degree of precision.

The most important limitation of the method is that it has difficulty accounting for Pauli’s exclusion principle. The true wavefunction $\Psi$ must be antisymmetric, which generally means it has negative values in some regions, but it’s being represented by probabilities which are always positive. This can be fixed by labelling each particle with some positive or negative value, a “weight”, so that the estimated value of $\Psi_t$ is the expected value of the sum of all the particle weights in that region instead of just the expected number of particles. (Using these weights can also help to reduce noise even when the wavefunction is positive everywhere.) It is not a complete solution however. There can be additional spurious wavefunctions that are not antisymmetric and have even lower energies than the true ground state, so that the contributions of these spurious states grows faster than the contribution of the true ground state. If the contribution of the correct, antisymmetric, ground state is held constant, the amounts of positive and negative particles both grow without bound and although in theory their weights cancel out on average, the amount of noise and amount of computational resources the simulation takes both increase exponentially. To prevent this, positive and negative particles must be allowed to annihilate each other. The labels are not really negative probabilities after all, so some artificial means of cancelling out must be included. This only works though if the density of each is high enough that this annihilation happens often enough to keep the spurious ground state in check. Since the density of particles must remain above a certain level, the number of particles necessary is about proportional to the size of the region of phase space which has a non-negligible value of the wavefunction. The dimension of the phase space is proportional to the number of physical particles, so its size (and therefore the number of particles needed) increases exponentially as the number of physical particles increases. This makes this method impractical except for systems with a very small number of electrons.

Another option for ensuring antisymmetry is to use some approximation to the wavefunction as a starting point, and not allow the particles to leave the region where this approximation is positive (in the simplest implementation, this involves simply deleting any particles which leave the region, but more advanced implementations may move them away from the boundary). If the approximate wavefunction you start with is antisymmetric, this ensures that antisymmetry is respected. This allows the simulation of much larger systems than the previous method, but it introduces an additional approximation. The wavefunction found is the lowest-energy one that has the same zeroes as the input wavefunction, so in general it is better than simply using the input wavefunction itself, but it still isn’t generally the true ground state.

The other solution, which is simplest, is to just only consider systems of just one or two electrons, where the Pauli exclusion principle doesn’t matter (two is possible because their spins can be different). This is the approach I will be taking here, with larger systems simulated with more approximate but faster methods instead.

There are some additional more minor sources of error as well, but they are much less important than the first two. For one, the method used to keep the number of particles stable can introduce a bias because when most of the particles happen to be in low-energy configurations, the number of particles increases and eventually must be artificially reduced, which biases the system against these low-energy regions, biasing the overall energy estimate up a little. Another possible source of error is the finite time-steps used to simulate random motion, which can be a particular problem when the electrons happen to come very close to the nuclei. There are methods of mitigating both of these sources of bias. Of course, there is also the possibility of physical effects the simulation simply doesn’t take into account, such as the magnetic interactions, the non-zero size of the nuclei, relativistic effects, and sometimes the motion of the nuclei.

Results

All of these results are produced by this program. For comparison, and to check the accuracy of the simulation, I tested it with some 3D systems with known energies.¹ All values are in natural units.

The level of accuracy isn’t necessarily the same between 3D and 4D, because the 4D atoms are inherently more difficult to simulate, but this should give a rough idea. I suspect that the main reason for the disagreement of bond lengths might be the reference values I used using a different definition of bond length (energy minimum with fixed nuclei rather than average distance with realistic nuclei), since I got a value closer to the reference value when I re-ran the program with much higher nuclear masses, but I’m not sure as the references didn’t make their definition explicit. The variances on the calculated bond lengths were still rather higher than on the energies (although I didn’t add the program feature to calculate the bond length random error until part way through running these simulations which is why those random errors aren’t listed).

For these 4D simulations, I have used an electric constant of 0.9. For the simplest case, the hydrogen atoms, it is possible to solve the Schrödinger Equation directly, which gives the reference values for those cases. For the other systems, the diffusion monte carlo simulation is the best I have. In the 4D case, I have separated out different isotopes because they are significantly different, unlike in 3D.

The units aren’t really comparable between 3D and 4D, because it’s necessary to derive the natural units in different ways, so the fact that all of the energies are much smaller isn’t significant. What is more significant is the ratios. Several major differences from 3D stand out.

Hydrogen 1 (protium) and hydrogen 2 (deuterium) are very different from each other, with protium having about 3 times the ionization energy of deuterium, as well as significantly shorter and stronger bonds. This is due to the s-force repulsion between the neutron and electron. In protium the overall potential remains attractive at small distances, whereas in deuterium there is a small region around the nucleus which the electron is repelled from. The difference between helium 3 and helium 4 is smaller.
Neither hydrogen isotope seems to have a stable negative ion, with the anion energies reported by the simulation being within the random error of the energies of the uncharged atoms. Whenever I run simulations of these ions it is also evident that one of the electrons detaches and drifts away, in one case to over 1000 units away. It is difficult to prove that there isn’t some very weak bond remaining between the electron and the atom, but it seems unlikely. The attraction potential between an electron and an uncharged atom due to the atom’s polarizability decreases as 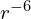$r^{-6}$ , so it quickly becomes negligible as the electron gets farther away.
The bond energies are extremely high relative to the ionization energies. In 3D, even the strongest covalent bonds (in carbon monoxide) have somewhat less energy than the lowest ionization energies for single atoms (caesium). In 4D, in contrast, not only are some of the bond energies greater than the ionization energies, they’re greater for the same elements, and this is just the first two elements, not even ones picked for particularly strong bonding.

All of these, I think, can be intuitively explained by the fact that the electrons in isolated protium and deuterium atoms just aren’t very strongly bound. The potential energy in 4D protium is around $2 \times 10^{-2}$ , or 5 times the total energy, which is much lower because the negative potential energy is almost entirely cancelled out by the positive kinetic energy. In both 4D helium and 3D hydrogen, the potential energy is only about twice the total energy (or exactly twice in 3D hydrogen). $2 \times 10^{-2}$ is therefore in a sense the natural energy scale of this atom, even though it’s much higher than the actual energy. The bond energy of diprotium is still much smaller than the total energy of helium for example, so it’s not that the bond energy is exceptionally high, it’s just that protium is unusually easy to ionize. This also seems to explain why deuterium’s energy is so much lower, that the weak binding is easy to disrupt, and why the negative ions aren’t stable, because these nuclei are barely even able to hold one electron. As for why the potential and kinetic energies are so nearly balanced, I have some thoughts but that’s beyond the scope of this post.

Another heuristic explanation for why the bond energy is so high relative to the ionization energy (which like the rest of these I don’t really have a way of making rigorous but which sounds right to me) is that when an electron is already held in place by one nucleus, giving it some kinetic energy, it can be affected by the potential of the second nucleus even without the wavefunction becoming much more spatially localized, so the increase in potential energy is larger than the increase in kinetic energy, and if they initially mostly cancel out, this effect of bonding causes them to be less balanced.

One other part of these results that surprised me was how short the bond in dideuterium is. Despite the fact that each nucleus has a small region around it the electrons are unable to enter, each nucleus is still well within the atomic orbital of the other atom.

https://physics.nist.gov/PhysRefData/ASD/ionEnergy.html ↩︎
https://zenodo.org/records/1233707 ↩︎
Herzberg, G., & Jungen, C. (1972). Rydberg series and ionization potential of the H2 molecule. Journal of Molecular Spectroscopy, 41(3), 425–486. doi:10.1016/0022-2852(72)90064-1 ↩︎
https://cccbdb.nist.gov/exp2x.asp?casno=1333740&charge=0 ↩︎
Apparently this value comes from Lide, David R., ed. (2006). CRC Handbook of Chemistry and Physics (87th ed.). Boca Raton, FL: CRC Press. ISBN 0-8493-0487-3., but I’m just trusting that https://en.wikipedia.org/wiki/Hydrogen is using that reference correctly because I can’t be bothered finding that book in a library. ↩︎

1
I tested the program a while ago with some of these molecules to see that it was generally accurate, then generated all the values shown in the table before looking up the final reference values (although I remembered roughly what some of them should be). After looking up the reference values I realised some ways I could have made the simulations more accurate (such as using the correct nuclear masses for the monatomic systems) but I left it as is according to the original plan to avoid cherry-picking.

System	Energy (ref)	Energy (sim)	Bond length (ref)	Bond length (sim)
$\ch{H}$	$-0.49973$ ¹	$-0.50001(23)$
$\ch{H^-}$	$-0.52745$ ²	$-0.52838(69)$
$\ch{H_2^+}$	$-0.5971$ ³	$-0.59739(26)$	$1.990$ ⁴	$2.091$
$\ch{H_2}$	$-1.1654$ ⁵	$-1.1642(12)$	$1.401$	$1.500$
$\ch{He}$	$-2.903385$	$-2.9036(22)$

System	Energy (true)	Energy (sim)	Bond energy/ electron affinity (sim)	Bond length (sim)
$\ch{^1H}$	$-3.954\times 10^{-3}$	$-3.915(85)\times 10^{-3}$
$\ch{^2H}$	$-1.389\times 10^{-3}$	$-1.378(74)\times 10^{-3}$
$\ch{^1H^-}$		$-3.936(24)\times 10^{-3}$	$-1.8(2.4) \times 10^{-5}$
$\ch{^2H^-}$		$-1.394(44)\times 10^{-3}$	$0.5(4.4) \times 10^{-5}$
$\ch{^1H_2^+}$		$-7.051(91)\times 10^{-3}$	$3.097(91) \times 10^{-3}$	$9.4$
$\ch{^1H_2}$		$-1.443(54)\times 10^{-2}$	$6.52(54) \times 10^{-3}$	$7.6$
$\ch{^2H_2}$		$-5.23(13)\times 10^{-3}$	$2.45(13) \times 10^{-3}$	$11.7$
$\ch{^3He}$		$-8.584(41)\times 10^{-2}$
$\ch{^4He}$		$-5.5538(99)\times 10^{-2}$

Derivation

Limitations

Results

Comments

Leave a Reply Cancel reply