The internal details of the nuclei are mostly not very relevant to chemistry, since they are so much smaller than normal electron orbitals that they can usually be treated as point-like. However, nuclear physics is what determines which elements exist at all, and in what quantities, so I’ve been thinking a bit about how it would work in my 4D world and how this might influence which elements are dominant on rocky planets like Earth.
The 3D Case
This chart shows the abundances of the elements in the solar system, as measured in real life. It’s on a log scale, so the elements at the bottom are billions of times rarer than those at the top. There are a few trends to note.
- Hydrogen and helium, the first two elements, are far more common than everything else. This is because they were the original elements created in large quantities in the big bang.
- After that, there’s a general trend towards later elements being less common. Heavier elements are built up from lighter elements, so this makes sense.
- Elements with even atomic numbers are more common than those with odd atomic numbers, since they are more stable. Protons like to form pairs of opposite spin. For the elements up to around iron, this is also because they are built up from helium-4. Any environment hot and dense enough to fuse helium into heavier elements is likely to have already fused all of its hydrogen into helium, which is particularly stable. To get around this requires beta decay, which is only possible in certain cases.
- Lithium, beryllium and boron are unusually rare for their small size, since the same conditions capable of producing them are also usually capable of destroying them so nucleosynthesis tends to skip straight from helium to carbon via the triple-alpha process.
- There’s a bit of a peak around iron. These are the most stable nuclei, so fusion beyond this point stops providing energy therefore it sometimes proceeds to this point before stopping. Similarly there’s a small peak at lead, the last stable element, where the s-process that creates some of the heavier elements gets stuck.
Making a rocky planet requires further processing that alters the abundances from their initial ratios depending on the chemical properties. For the top 9 most common elements cosmically:
- Hydrogen and helium are highly volatile, so they remained gaseous in the inner solar system and did not become trapped in the rocky planets in large quantities as they formed. They are so light that even if they end up in a planet’s atmosphere, it is easy for them to get blown away into space.
- Oxygen on its own is a gas, but it bonds easily to other elements like silicon to form solids. Carbon itself is solid but it has several gaseous compounds with other common elements.
- Nitrogen and neon are highly volatile.
- And finally, iron, silicon and magnesium have low volatility and form rock.
The Earth therefore ended up with silicon, iron, oxygen and magnesium as its main constituents. The iron is much denser than the rest of these, and mostly sank to the core, taking with it the majority of any trace elements soluble in it. Silicon and oxygen are the main components making up the crust, and a large proportion of rocks are some sort of silicate, sometimes with a bit of magnesium, iron, calcium and so on. Sometimes less common elements end up getting concentrated in specific minerals, and other times they are spread as trace components in other rocks, but I don’t have a good understanding of the factors that influence this.
The 4D Case
I expect many of the same factors determining the abundances of the elements in real life would apply in 4D too. There is an additional force to consider though, the s-force, which should have an effect on the nucleus just like the electromagnetic force does. I assume the weak reaction ![]() remains possible, and preferably it should conserve the s-charge (I don’t think this is stricly necessary because the corresponding boson is massive and there is therefore no gauge symmetry, but it seems neater to have the charge conserved anyway). The electron has a positive s-charge and the neutrino has no charge of any kind (otherwise it would interfere with the chemistry), therefore the neutron has to have some s-charge. The most elegant model is to have the neutron and electron have the same charge and for the proton to have no charge, but I’m not sure I want the electrons interacting significantly with each other through the s-force. To avoid that, I’d need the nucleons to have a much greater charge than the electrons, with the neutrons slightly more charged than the protons to keep the weak reaction balanced.
remains possible, and preferably it should conserve the s-charge (I don’t think this is stricly necessary because the corresponding boson is massive and there is therefore no gauge symmetry, but it seems neater to have the charge conserved anyway). The electron has a positive s-charge and the neutrino has no charge of any kind (otherwise it would interfere with the chemistry), therefore the neutron has to have some s-charge. The most elegant model is to have the neutron and electron have the same charge and for the proton to have no charge, but I’m not sure I want the electrons interacting significantly with each other through the s-force. To avoid that, I’d need the nucleons to have a much greater charge than the electrons, with the neutrons slightly more charged than the protons to keep the weak reaction balanced.
In either case, the total electric + s-force between two neutrons is similar to between two protons, so the tendency that exists in real life for heavy nuclei to be more stable if they have a greater number of neutrons to protons would not exist. Also in both cases, since the neutrons have charges, nuclides with the same number of protons and different numbers of neutrons would have significantly different chemistry, to the point where they might as well be considered completely different elements rather than merely isotopes. This makes things more complicated, but I quite like it anyway because it means I have more elements to play with and I don’t have to commit to a single value of the ratio of the electric and s-force strengths.
This also means that for elements with a sufficiently high ratio of protons to neutrons, the electric force could overcome the s-force entirely and cause electrons to fall into the nucleus and be absorbed, converting it to a different element, effectively rendering that element unstable.
Model 1: Only Neutrons Charged
First let’s consider what this implies about the model where the proton has no s-charge. Rapid electron capture happens to all elements with strictly more protons than neutrons, cutting off half of all the possible elements. For elements with an equal number of protons and neutrons, the total potential near the nucleus scales like ![]() and remains attractive but not so attractive that stable orbits are impossible, similar to the 3D case, but for elements other than hydrogen at most a single electron can occupy this position at a time because of the repulsive forces between the electrons. For elements like helium-4 and lithium-6, there may be some noticable amount of mixing between this small 1s orbital and the other orbitals at radii greater than 1, but as the atomic number increases, this electron gets progressively closer to the nucleus while all the other electrons remain far enough away to avoid the repulsive s-force, therefore these elements would end up very similar to the elements with one less proton and one more neutron, as though the inner electron were absorbed into the nucleus entirely.
and remains attractive but not so attractive that stable orbits are impossible, similar to the 3D case, but for elements other than hydrogen at most a single electron can occupy this position at a time because of the repulsive forces between the electrons. For elements like helium-4 and lithium-6, there may be some noticable amount of mixing between this small 1s orbital and the other orbitals at radii greater than 1, but as the atomic number increases, this electron gets progressively closer to the nucleus while all the other electrons remain far enough away to avoid the repulsive s-force, therefore these elements would end up very similar to the elements with one less proton and one more neutron, as though the inner electron were absorbed into the nucleus entirely.
Hydrogen-1 in particular is vulnerable to electron capture in this case, therefore a free neutron must be stable (or at least a hydrogen atom would act pretty much like a free neutron anyway). The major primordial element would then be element 0, neutronium, rather than hydrogen. Unlike in real life, neutronium still interacts significantly with normal matter because of the presence of the s-force, and it would chemically act much like an even more inert version of helium, without even the van der Waals force. Importantly, neutronium is also perfectly transparent to light (technically neutrons can scatter light because of their magnetic moments, but a rough calculation indicates this effect is so weak that even an entire star made of it would still be invisible). Given that this is what most of the universe is made of, it makes the interstellar medium (at least where there’s low metallicity) much more transparent. Stars made mostly of neutronium can only emit light through their other components, and clouds of neutronium that are collapsing under gravity cannot cool down by emitting light like clouds of hydrogen can. If they reach high enough temperatures, they can start emitting the form of radiation associated with the s-force instead, which I’ll call S bosons or s-rays, but because of the S boson’s rest mass, this cannot occur until temperatures where ordinary matter would be radiating x-rays (the exact cutoff depends on the fine structure constant which I haven’t decided yet, but assuming its value is similar to real life, this is about right) (this is why I can justify ignoring s-rays in most contexts where light is being considered). Depending on the abundance of heavier elements, this could be a significant impediment to star formation.1I’m assuming that gravity follows the inverse square law even though this is unnatural for 4D, because that way stable orbits are possible. The effective pressure of gravity on the surface of a collapsing cloud of gas is then proportional to ![]() , but the adiabatic index of a monatomic 4D gas is
, but the adiabatic index of a monatomic 4D gas is ![]() so the gas pressure increases like
so the gas pressure increases like ![]() if it can’t radiate away its heat. If a cloud of neutronium begins to collapse under its own gravity, it will therefore stop at a certain point once the gas pressure becomes high enough to overcome the strength of gravity, unless it contains enough heavier elements to be able to radiate away its heat or it is large enough that at its equilibrium size it is hot enough to produce s-rays. See Jeans Instability for how this works in real life.
if it can’t radiate away its heat. If a cloud of neutronium begins to collapse under its own gravity, it will therefore stop at a certain point once the gas pressure becomes high enough to overcome the strength of gravity, unless it contains enough heavier elements to be able to radiate away its heat or it is large enough that at its equilibrium size it is hot enough to produce s-rays. See Jeans Instability for how this works in real life.
The first fusion of neutrons (which, because of the s-force, still requires considerable activation energy) produces dineutrons which immediately decay to deuterium via beta decay. The repulsion between two deuterons is twice that between a deuteron and a neutron, so the next step is probably ![]() . Since this doesn’t require the weak force, this would proceed much faster than the first step. Similar to the case of neutronium, it is tritium not helium-3 that is stable. The next step might either be
. Since this doesn’t require the weak force, this would proceed much faster than the first step. Similar to the case of neutronium, it is tritium not helium-3 that is stable. The next step might either be ![]() ,
, ![]() ,
, ![]() , or something else, or it might stop there until the neutronium runs out and the temperature of the star rises. The way the analogous reactions work in real life is sufficiently unexpected to me that I can’t be confident of any such prediction.
, or something else, or it might stop there until the neutronium runs out and the temperature of the star rises. The way the analogous reactions work in real life is sufficiently unexpected to me that I can’t be confident of any such prediction.
Some of the main routes to producing much heavier elements in real life, past the point where fusion becomes endothermic, are the s and r processes, where free neutrons produced by other reactions are absorbed by heavy nuclei (which then sometimes beta decay to produce more protons). I assume the reason this process happens easily is because neutrons are not repelled by nuclei so there is little to no potential barrier, but this is not the case for 4D neutrons with an s-charge, so I these processes would be expected to occur at rates more similar to the p-process (the similar process but with protons instead of neutrons) in real life, which is rarer and requires higher temperatures. Elements too far beyond the iron peak cannot be generated in significant quantities by fusion of similar-mass nuclei because those reactions are thermodynamically unfavourable, so the unbalanced fusion of large nuclei with individual protons and neutrons (or possibly other small nuclei), which remain favourable much longer, are the only possible route. These require a specific combination of very high temperature with large quantities of unfused light nuclei, so I expect elements heavier than the equivalent of iron to be quite a bit rarer than in real life.
Model 2: both nucleons charged
Now let’s consider the case where the nucleons have a similar charge to each other and the electron’s charge is much less. It is still possible for elements with a sufficiently high ratio of electrons to neutrons to have the electrons fall into the nucleus and be absorbed, but the threshold ratio for this to happen depends on the parameters.
In simulations, I’ve found the nicest balance of properties near an s-force/electric force strength ratio of a little below 2. It would therefore be ideal to have this be the ratio associated with the most stable elements, with a similar number of protons and neutrons, which puts the threshold for electron capture at about 1 proton per nucleon, i.e. this only applies to hydrogen-1. I might as well set the threshold to exactly hit hydrogen-1, which leaves it stable but gives it unusual properties (similar to hydrogen-2 in the other model). This element is sufficiently unique I may write a whole post about it at some point. This leaves one free parameter left, the proton/electron s-charge ratio, but like the speed of light, it can just be set for now to be vaguely very high and the precise value doesn’t matter.
In this model, the s-force between any two nucleons is much larger than the electric force between two protons, so the latter can mostly be ignored. To make the nuclei stable, the strong force also has to be stronger to compensate, and this all has implications for overall rates of nuclear reactions, but it should be possible to compensate for that by changing the range of the strong force and thus the sizes of the nuclei. The main thing to keep in mind is making sure that the binding energies involved aren’t bigger than the rest masses of the nucleons, but there are lots more free parameters left to tweak to make sure that works.
The main differences between this model and the other one when it comes to nucleosynthesis and which elements are stable are that elements with more protons than neutrons become stable and that all nucleons repel each other near equally (neutrons just slightly more), rather than only nucleons of the same type repelling each other. This makes a wider range of proton/neutron ratios stable, and also changes the steps involved in fusing hydrogen into helium. The primordial element is now hydrogen-1 rather than neutronium, which fuses like ![]() . Now it is helium-3 not hydrogen-3 that is stable, so the next step is probably
. Now it is helium-3 not hydrogen-3 that is stable, so the next step is probably ![]() . In real life the next step is for the helium-3 to fuse with either more helium-3 or helium-4, but with the neutrons also contributing to the repulsion, the potential barrier is 9 or 12 times greater than for two protons to fuse (neglecting the difference in radius between hydrogen and helium), rather than 4 times like in real life, so I’m not sure if it would happen immediately or not.
. In real life the next step is for the helium-3 to fuse with either more helium-3 or helium-4, but with the neutrons also contributing to the repulsion, the potential barrier is 9 or 12 times greater than for two protons to fuse (neglecting the difference in radius between hydrogen and helium), rather than 4 times like in real life, so I’m not sure if it would happen immediately or not. ![]() probably still doesn’t happen much because it both requires a weak interaction and has a large-ish potential barrier, unless
probably still doesn’t happen much because it both requires a weak interaction and has a large-ish potential barrier, unless ![]() is somewhat stable which seems unlikely. Alternatively, if tritium is stable, it could reasonably easily fuse with hydrogen-1 to helium-4.
is somewhat stable which seems unlikely. Alternatively, if tritium is stable, it could reasonably easily fuse with hydrogen-1 to helium-4.
Like in the other model, the neutron-capture processes are suppressed and heavy elements are very rare.
Comparison
Model 1 has neutronium as the most common form of matter in the universe, which is weird and cool, and the symmetry between neutrons and protons is appealing. On the other hand, model 2 has more elements, and it feels like less of a deviation from real life. While exotic new things are cool, this whole project is an exercise in exploring what chemistry would be like in 4D, and part of that premise is seeing how things turn out with a minimal amount changed to turn real life physics 4D. Both models have one weird small isotope of hydrogen and one more normal-sized isotope, even though which isotope is which depends on the model, so this doesn’t count as a pro or con of either. Although I haven’t discussed it much here, the most crucial advantage of model 2 is that the elements it produces have more interesting and varied chemistry. For this reason, I intend to proceed with model 2 from now on.
Organic Elements and the Triple-Alpha Process
Some of the elements with the most interesting and varied chemistry, or at least the most thoroughly explored in real life because they’re so relevant to biology, are the first p-block elements, carbon, nitrogen and oxygen (technically boron, flourine and neon are also part of the first p-block, but B and F are much less abundant than these three and Ne is inert, so they are not so relevant). In 4D, the first p block is elements 5 through 12. (I’m ignoring the neutron numbers here because although they differ much more than real life isotopes, 4D isotopes are still similar enough that it will not affect this discussion. Also I don’t have the simulations on them to back it up yet.) 3D carbon has atomic number 6, but its main distinguishing property is that it has the second shell half full giving it a particularly high valency, a property shared by 4D element 7 instead of 6. Element 7, with an odd atomic number, would be expected to be less common than elements 6 and 8, so perhaps chains alternating between elements 6 and 8, like 3D boron nitride, would take the place of element 7 as the core component in 4D organic chemistry. On the other hand, element 8 (or at least some of its isotopes) might form such a strong quadruply bonded diatomic molecule that it becomes difficult for life to convert it to any other form (kind of like ![]() in 3D). Nitrogen does have an unusually high abundance for an odd element, a fact that I don’t have a very good explanation for, so I’m not sure whether this would apply to 4D element 7 too.
in 3D). Nitrogen does have an unusually high abundance for an odd element, a fact that I don’t have a very good explanation for, so I’m not sure whether this would apply to 4D element 7 too.
The synthesis of carbon in real life is almost entirely by the triple-alpha process, which depends on a coincidental resonance between the energy of three helium-4 nuclei and an excited state of carbon-12. There is no reason to expect this same resonance would exist in 4D. Given I’m not able to do the simulations that would prove whether it exists or not (even cutting edge scientists with access to experimental data which doesn’t exist for 4D struggle to simulate nuclear physics in large nuclei) and there are a bunch of remaining free parameters, I could just assume it does exist. If you believe that, whether through the anthropic principle, divine intervention, or some other method, this resonance exists because it is necessary to make carbon, including it in an alternative model of physics could be interpreted as sticking to making minimal changes. For me though, it’s probably simpler to just assume that beryllium-8 is stable in 4D (or at least decays in some way other than alpha emission) which would provide an alternative route to heavier elements with no resonances. This means there’s less of a gap between stars that can only fuse hydrogen to helium and those that can fuse heavier elements, and there probably isn’t the peculiar lack of elements 3, 4 and 5 that exists in real life.
Iron and Lead
The sizes of the most stable element and the last stable element (iron and lead in real life) depend on the ratio of the strong force to the repulsive forces that prevent large nuclei from being stable. The strength of the strong force in my model has not yet been determined, so which elements these are is still a free parameter, but the two quantities are linked.
The binding energy of an element can be approximated in the liquid drop model by
The ![]() term includes the strong force between adjacent nucleons as well as the kinetic energy. The offset
term includes the strong force between adjacent nucleons as well as the kinetic energy. The offset ![]() is a correction to account for the fact that nucleons on the surface of the nucleus have fewer adjacent nucleons to be attracted to. The
is a correction to account for the fact that nucleons on the surface of the nucleus have fewer adjacent nucleons to be attracted to. The ![]() term is the s and electric forces, which extend all the way across the nucleus rather than only affecting adjacent nucleons. There are usually more terms than this included, to account for the differences between even and odd nuclei and the effect of the ratio of protons to neutrons, but I don’t need the detail provided by the even/odd term here and I’ll be focusing only on nuclei with about the same number of protons and neutrons.
term is the s and electric forces, which extend all the way across the nucleus rather than only affecting adjacent nucleons. There are usually more terms than this included, to account for the differences between even and odd nuclei and the effect of the ratio of protons to neutrons, but I don’t need the detail provided by the even/odd term here and I’ll be focusing only on nuclei with about the same number of protons and neutrons.
The value of ![]() depends on the proportion of bonds surface nucleons are missing, how the range of the strong force compares to its equilibrium distance, and how the strength of the strong force compares to the kinetic energy of the nucleons. Picking some rough guesses for these gives
depends on the proportion of bonds surface nucleons are missing, how the range of the strong force compares to its equilibrium distance, and how the strength of the strong force compares to the kinetic energy of the nucleons. Picking some rough guesses for these gives ![]() , so I’ll be using that value. The value of
, so I’ll be using that value. The value of ![]() doesn’t matter for which nuclides are stable so long as the ratio of
doesn’t matter for which nuclides are stable so long as the ratio of ![]() to
to ![]() is fixed because it doesn’t affect the relative order of the energies, only the overall scale, so I’ll fix
is fixed because it doesn’t affect the relative order of the energies, only the overall scale, so I’ll fix ![]() . The most stable atomic number is simply the value of
. The most stable atomic number is simply the value of ![]() where
where ![]() is highest. If
is highest. If ![]() , then the element with that value of
, then the element with that value of ![]() is theoretically suceptible to spontaneous fission, but many such elements in real life are stable in practice because the half-lives are so long they can’t even be measured. A more reasonable criterion for instability would be
is theoretically suceptible to spontaneous fission, but many such elements in real life are stable in practice because the half-lives are so long they can’t even be measured. A more reasonable criterion for instability would be ![]() , which indicates suceptibility to alpha emission. As
, which indicates suceptibility to alpha emission. As ![]() tends to infinity, the atomic numbers of the most stable element and heaviest stable element grow like
tends to infinity, the atomic numbers of the most stable element and heaviest stable element grow like ![]() and
and ![]() respectively, although
respectively, although ![]() has to be quite large before these become good approximations.
has to be quite large before these become good approximations.
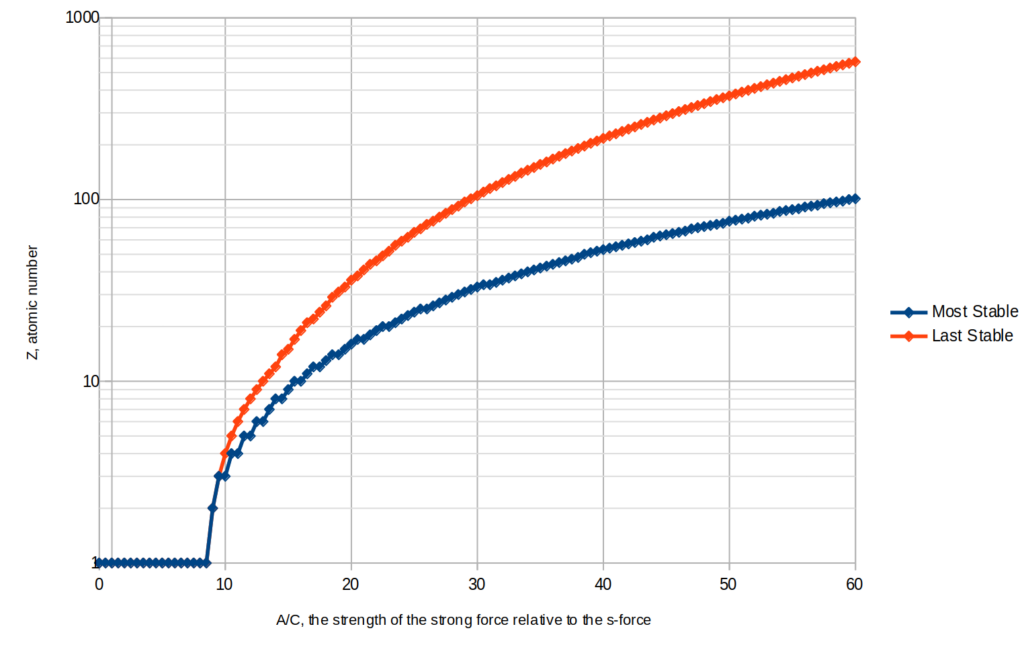
The chart shows the results for various values of the parameter A. This is only a rough approximation, especially since the liquid drop model is a very bad approximation for the binding energy of an alpha particle, but it should be good enough to get a rough idea of how many common elements there are and how many elements there are that are stable at all. The number of elements is still much greater than the atomic number limit though, since there are all the different isotopes too.
One of the factors that affects nucleosynthesis in real life is the fact that heavy elements have a different ratio of neutrons to protons than light elements, so fusing together light nuclei in many cases can’t produce stable heavier nuclei without some electron captures or ![]() decays to convert some of the protons to neutrons. This does not apply in 4D, since the most stable elements of all masses have approximately balanced amounts of neutrons and protons. One of the processes this influences is what creates the high abundance of iron peak elements. Helium-4 can fuse exothermically (though not very) with any element up to cerium, atomic number 58. The overall limit of how big a nucleus can be before adding helium-4 cannot produce energy is around lead, as the approximation used above suggests, but for elements beyond cerium it tends to require the starting isotope to be neutron-rich. The data this is based on can be found here, under the
decays to convert some of the protons to neutrons. This does not apply in 4D, since the most stable elements of all masses have approximately balanced amounts of neutrons and protons. One of the processes this influences is what creates the high abundance of iron peak elements. Helium-4 can fuse exothermically (though not very) with any element up to cerium, atomic number 58. The overall limit of how big a nucleus can be before adding helium-4 cannot produce energy is around lead, as the approximation used above suggests, but for elements beyond cerium it tends to require the starting isotope to be neutron-rich. The data this is based on can be found here, under the ![]() tab. Cerium is not common though, which I get the impression is for two reasons. Just successively adding helium-4 can only produce nuclei with equal numbers of protons and neutrons, and beyond nickel-56 those become so unstable they’re unlikely to form, or at least are easily destroyed when they do. The other reason is that in an environment which is hot enough to fuse helium into larger nuclei, fusing helium with itself happens so rapidly that practically the only helium present is that generated by larger nuclei being disintegrated by the heat. Such an environment leads to an equilibrium of nuclei forming and being destroyed, which can only tend in the direction of thermodynamic equilibrium, that is in the direction of the most stable nuclides or (at very high temperatures) even smaller nuclides than that. This latter factor still applies in 4D, but the former doesn’t, which suggests the fall off in abundance on either side of the most stable elements might be somewhat more gradual than in real life.
tab. Cerium is not common though, which I get the impression is for two reasons. Just successively adding helium-4 can only produce nuclei with equal numbers of protons and neutrons, and beyond nickel-56 those become so unstable they’re unlikely to form, or at least are easily destroyed when they do. The other reason is that in an environment which is hot enough to fuse helium into larger nuclei, fusing helium with itself happens so rapidly that practically the only helium present is that generated by larger nuclei being disintegrated by the heat. Such an environment leads to an equilibrium of nuclei forming and being destroyed, which can only tend in the direction of thermodynamic equilibrium, that is in the direction of the most stable nuclides or (at very high temperatures) even smaller nuclides than that. This latter factor still applies in 4D, but the former doesn’t, which suggests the fall off in abundance on either side of the most stable elements might be somewhat more gradual than in real life.
Combining all this together, we get the following trends for elemental abundances (including only atomic number not neutron number because a 3D chart would be less clear).

There’s no calculation at all behind this chart, nor any detailed reasoning beyond what I’ve already explained. I would like to emphasise that just because there are numbers here doesn’t mean you should take them seriously, it’s just a guess meant to illustrate the bits of this topic that I do somewhat understand.
The features illustrated in the chart are explained throughout this post, but to summarise:
- The iron peak and stable limit occur at higher atomic numbers (since I’ve selected a value of the parameter A that is most suitable for the range of chemistry I’m expecting)
- The iron and lead peaks both still exist, but the iron peak is broader than in real life. (The fact that I’m calling them “iron” and “lead” here does not mean they are necessarily chemically similar to these elements.)
- The drop in abundances of elements heavier than the most stable one is much bigger than in real life.
- It is only hydrogen, not helium too, that has an exceptionally high abundance.
- Elements 3,4, and 5 are on trend rather than being unusually rare.
- Even elements being more abundant than odd ones is still the case, and there is some additional local variation I’ve just simulated with random numbers for the chart.
- 1I’m assuming that gravity follows the inverse square law even though this is unnatural for 4D, because that way stable orbits are possible. The effective pressure of gravity on the surface of a collapsing cloud of gas is then proportional to
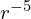 , but the adiabatic index of a monatomic 4D gas is
, but the adiabatic index of a monatomic 4D gas is 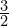 so the gas pressure increases like
so the gas pressure increases like 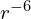 if it can’t radiate away its heat. If a cloud of neutronium begins to collapse under its own gravity, it will therefore stop at a certain point once the gas pressure becomes high enough to overcome the strength of gravity, unless it contains enough heavier elements to be able to radiate away its heat or it is large enough that at its equilibrium size it is hot enough to produce s-rays. See Jeans Instability for how this works in real life.
if it can’t radiate away its heat. If a cloud of neutronium begins to collapse under its own gravity, it will therefore stop at a certain point once the gas pressure becomes high enough to overcome the strength of gravity, unless it contains enough heavier elements to be able to radiate away its heat or it is large enough that at its equilibrium size it is hot enough to produce s-rays. See Jeans Instability for how this works in real life.
Leave a Reply