Cross Products and Bivectors
Magnetic fields, magnetic moments, magnetisations and so on are generally considered to be vectors (or vector fields). In 3D, this description works fine, and formulae relating magnetic fields to anything else just need to use cross products. For example, two of Maxwell’s equations are
where in both directions, going between ![]() and
and ![]() requires the cross product. In 4D, there is no cross product, so we’ll have to generalise our description magnetism first.
requires the cross product. In 4D, there is no cross product, so we’ll have to generalise our description magnetism first.
Rather than considering the magnetic field to be a vector, we can instead describe it as a bivector. Formally, a bivector is an antisymmetric rank 2 tensor, but you can imagine it as sort of representing a relation between two directions. Just like a vector can be pictured as a line of a certain length in a certain direction, a bivector can be pictured as a surface of a certain area oriented a certain way. The most familiar example of a bivector would be something like angular velocity. Just like the magnetic field, it is usually called a vector, but the direction of that vector, the axis of rotation, is the one part of the space that isn’t moving. It is the two other axes that are moving. Bivectors in 3D are sometimes also called axial vectors.
Given two vectors ![]() and
and ![]() of any dimension, we can multiply them together to get the bivector
of any dimension, we can multiply them together to get the bivector ![]() , with the relation
, with the relation ![]() and therefore
and therefore ![]() . We can get back to vectors with another multiplication
. We can get back to vectors with another multiplication ![]() or in reverse
or in reverse ![]() (I’m not sure what the standard notation for this operation is though). Both of these are analogous to the cross product in the 3D case when vectors and bivectors are being identified, but with a change of sign (i.e.
(I’m not sure what the standard notation for this operation is though). Both of these are analogous to the cross product in the 3D case when vectors and bivectors are being identified, but with a change of sign (i.e. ![]() ). This is pretty much a drop-in replacement for the cross product. The formulae from earlier become
). This is pretty much a drop-in replacement for the cross product. The formulae from earlier become
(it may also be convenient to change the sign convention for ![]() in this case, but I’m not sure whether that causes more problems elsewhere so I won’t for now.)
in this case, but I’m not sure whether that causes more problems elsewhere so I won’t for now.)
In the 3D case, while this offers some conceptual clarification and leads in to the electromagnetic field tensor ![]() , it is pretty much just using slightly more obscure notation to express the same thing. Vectors and bivectors can be identified because if there is a basis of three unit vectors
, it is pretty much just using slightly more obscure notation to express the same thing. Vectors and bivectors can be identified because if there is a basis of three unit vectors ![]() , there are also three unit bivectors
, there are also three unit bivectors ![]() , so they can just be identified with each other. In 4D, this is not the case. There are of course four unit vectors
, so they can just be identified with each other. In 4D, this is not the case. There are of course four unit vectors ![]() , but there are six unit bivectors
, but there are six unit bivectors ![]() so they can’t be matched up. There is no cross product but most of the same formulae continue to work if the products
so they can’t be matched up. There is no cross product but most of the same formulae continue to work if the products ![]() involving the bivector versions of magnetic quantities are used.
involving the bivector versions of magnetic quantities are used.
Double Rotations
In 3D, every bivector (other than ![]() ) has a unique axis it is perpendicular to, and can be expressed as the product of two vectors. Not so in 4D. A bivector like
) has a unique axis it is perpendicular to, and can be expressed as the product of two vectors. Not so in 4D. A bivector like ![]() occupies all four axes at once
occupies all four axes at once
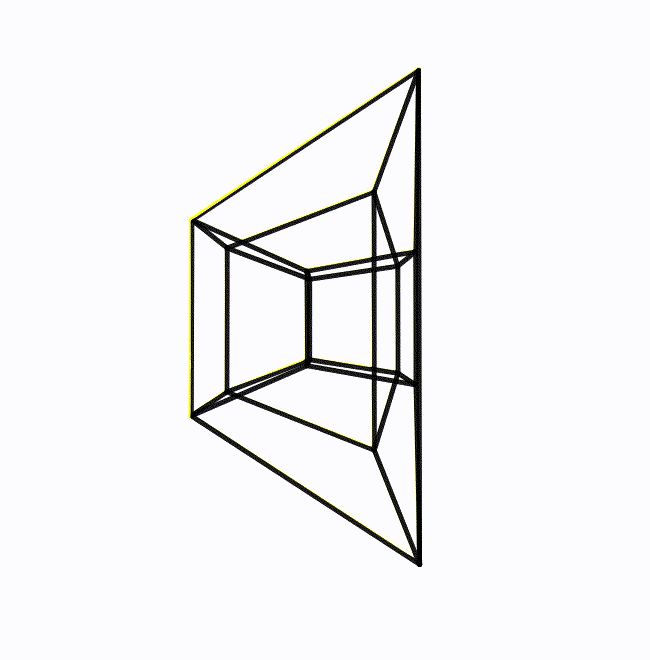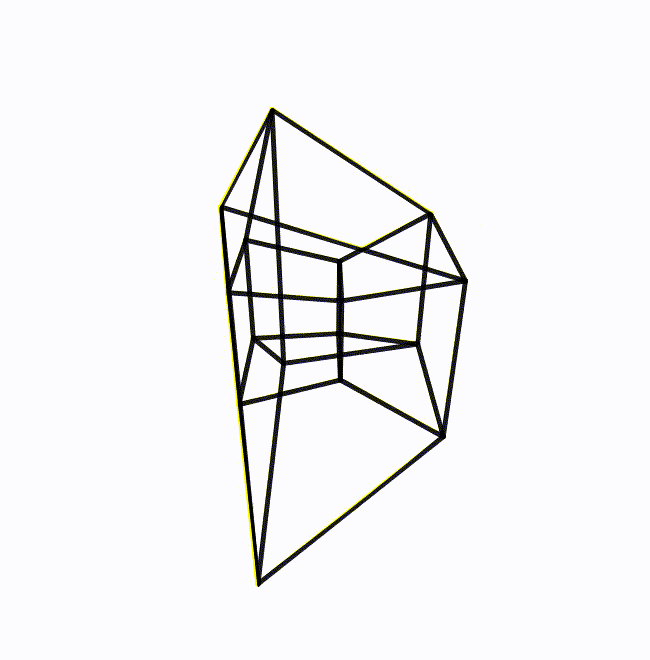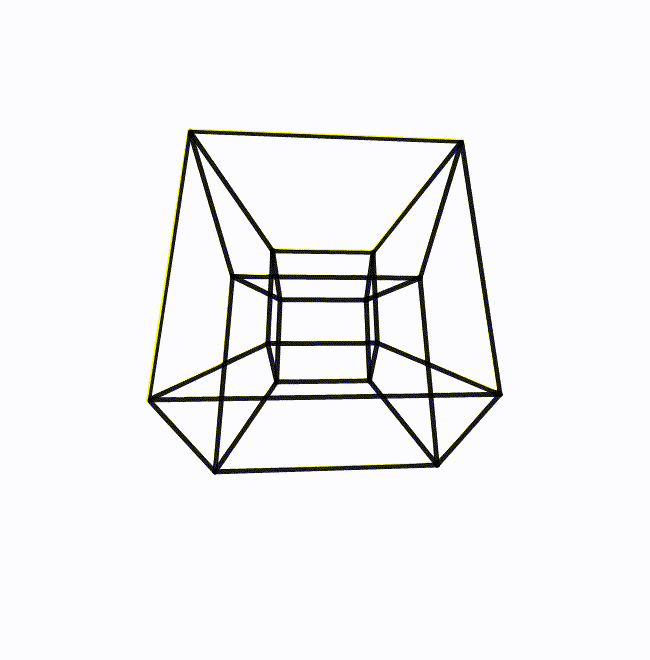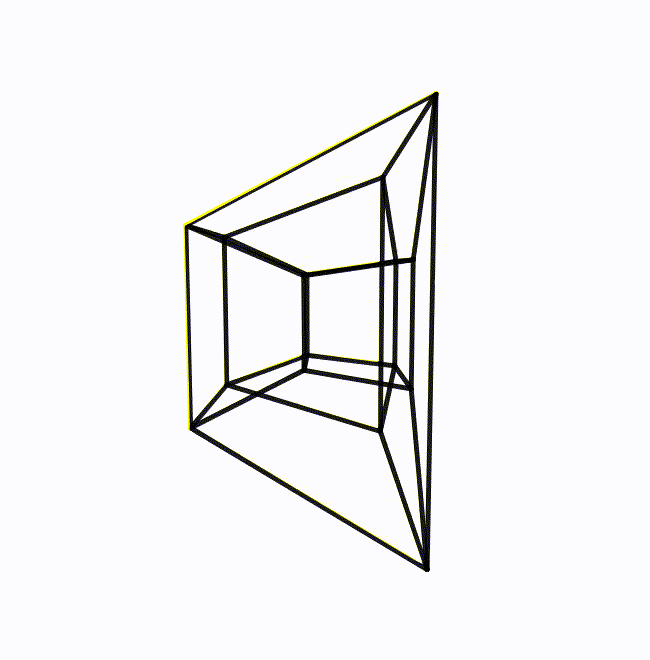
The animation shows an example of a double rotation (of a wireframe hypercube), a rotation where the angular velocity is such a bivector that includes every axis. The rotations in the two planes are essentially independent of each other. In the image, the hypercube rotates twice as fast in one plane as the other, but if the two rotations are equal in magnitude, the bivector becomes particularly symmetrical. No axis is distinguishable from any other. These bivectors are called isoclinic. For example, the bivector ![]() mentioned earlier can equivalently be expressed as
mentioned earlier can equivalently be expressed as ![]() . To be more precise about what I mean by there being no preferred axis, for any isoclinic bivector
. To be more precise about what I mean by there being no preferred axis, for any isoclinic bivector ![]() and non-zero vector
and non-zero vector ![]() , there are perpendicular vectors
, there are perpendicular vectors ![]() such that
such that ![]() .
.
In contrast, there are no such bivectors in 3D (or any other odd dimension). Every 3D bivector ![]() has some perpendicular vector
has some perpendicular vector ![]() (its axis) such that
(its axis) such that ![]() cannot (non-trivially) be expressed in terms of
cannot (non-trivially) be expressed in terms of ![]() since every
since every ![]() is perpendicular to
is perpendicular to ![]() .
.
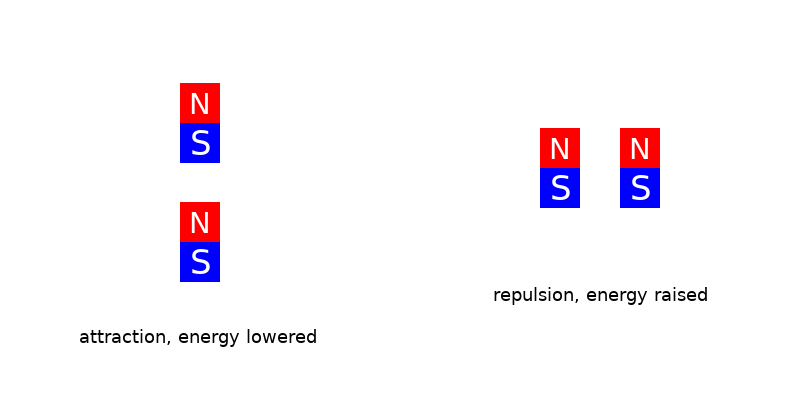
The relevance to magnetism is that if a magnetic dipole has an isoclinic magnetic moment, the field is uniform in every direction. The direction of the magnetic field varies, but its strength is simply proportional to ![]() , with no variation with angle. In the 3D case, every magnet has certain poles where the field is strongest, and similarly aligned magnets will tend to line up so that their poles are aligned. This is the reason why iron filings in a magnetic field tend to form little strings, and ferrofluids form spikes. The external magnetic field gives each particle a magnetic moment in the same direction, which causes an interaction between them that raises the energy if the particles are side by side, and lowers it if they are end to end. Some 4D magnets (if they aren’t isoclinic) could also have poles like this, but there would be a whole plane of poles rather than a single axis and the strength of the field would still be the same in every direction.
, with no variation with angle. In the 3D case, every magnet has certain poles where the field is strongest, and similarly aligned magnets will tend to line up so that their poles are aligned. This is the reason why iron filings in a magnetic field tend to form little strings, and ferrofluids form spikes. The external magnetic field gives each particle a magnetic moment in the same direction, which causes an interaction between them that raises the energy if the particles are side by side, and lowers it if they are end to end. Some 4D magnets (if they aren’t isoclinic) could also have poles like this, but there would be a whole plane of poles rather than a single axis and the strength of the field would still be the same in every direction.
Chirality and Intrinsic Magnetic Moments
Isoclinic bivectors fall into two classes, left and right handed. It is possible to transform between two bivectors in the same class by rotating and scaling, but to transform from one class to the other requires a reflection. One set is formed from linear combinations of ![]() ,
, ![]() , and
, and ![]() , and the other is generated by
, and the other is generated by ![]() ,
, ![]() , and
, and ![]() . Any bivector can be expressed as the sum of a left-handed part and a right-handed part, with the isoclinic bivectors being purely one or the other, and the bivectors contained in a single plane having each of their components of the same size. The dot product of two bivectors of opposite chiralities is always
. Any bivector can be expressed as the sum of a left-handed part and a right-handed part, with the isoclinic bivectors being purely one or the other, and the bivectors contained in a single plane having each of their components of the same size. The dot product of two bivectors of opposite chiralities is always ![]() . This dot product occurs in the formula
. This dot product occurs in the formula
describing the potential energy of a magnetic dipole of moment ![]() in a magnetic field
in a magnetic field ![]() . (The sign in this formula is different from usual because the square of a bivector is negative.)
. (The sign in this formula is different from usual because the square of a bivector is negative.)
This implies that if a magnetic field is purely left chiral, it has no direct interaction with right chiral dipoles, and vice versa. This is particularly odd since the formula for the field produced by a magnetic dipole involves reflecting about the vector between the point of measurement and the dipole, so the field has opposite chirality to the magnetic moment itself. Isoclinic magnetic dipoles do not interact magnetically at all with others of the same chirality.
As was demonstrated in the post on the fundamental properties of 4D electrons, their intrinsic magnetic moment is isoclinic, always with the same chirality, so the previous statement applies and static 4D electrons cannot interact magnetically with each other.
To see how this would affect macroscopic magnetic phenomena, let’s first briefly go through how the magnetic properties of materials arise from their electrons (the nuclei have magnetic moments too, but they are much smaller and can mostly be ignored).
Both the spin of an electron and its orbital angular momentum are associated with magnetic moments. In most chemicals, the electrons occur in pairs of opposite spins so that contribution cancels out and there is likewise no room for the electrons to move between different orbitals. In this case, there is no magnetisation in the absence of an applied field, and the only effect of an applied field is to slightly shift the orbitals in such a way as to produce a magnetisation opposite to the applied field, raising the energy and causing an interaction that repels the material from areas of high magnetic field. This effect is known as diamagnetism. It is present in all materials, but it is usually weaker than the other effects, so they will dominate the material’s magnetic properties if present. This is somewhat less true in 4D, since diamagnetism is not at all limited in which chiralities of fields it can interact with, unlike the other effects.
If a substance contains unpaired electrons, it can respond to the applied field by the electrons moving into states where their moments align with the applied field, either by changing their spins or by moving to different orbitals. This lowers the energy, attracting the material towards areas of high magnetic field, and is known as paramagnetism. In 3D, the paramagnetic effects of orbitals and spins behave rather similarly so there is not much need to distinguish between them, but in 4D, there is a significant difference that the orbital component can have any chirality and the spin component can only have one.
In cases where there are unpaired electrons, it is sometimes energetically favourable for the electrons on nearby atoms to have similar spins. If this effect is strong enough (and the temperature low enough), it can lead to large areas where the spins are all aligned, greatly increasing the response to an applied field, and making it possible for macroscopic objects to produce significant magnetic fields. This is known as ferromagnetism, and is the most familiar form of magnetic behaviour since it is so strong and obvious. It is present in iron and neodymium magnets for example.
In 3D, there are competing effects that tend to limit the strength of ferromagnets. At an atomic scale, exchange interactions cause the electrons spins of nearby atoms to align, but at larger scales, the magnetic effects become more important. Since aligned magnets side by side are energetically unfavourable, sufficiently large samples of ferromagnetic materials will have alternating domains where the magnetisation points in opposite directions, which gives the lowest energy overall. In the 4D case, since the magnetisation of a ferromagnet is entirely the result of the electrons’ intrinsic (spin) magnetic moments, there is no long-range magnetic interaction and, at least given sufficiently long annealing times, the entire crystal forms a single domain. It is plausible that samples of ferromagnetic materials would therefore naturally be fully magnetised even without having ever been exposed to an external magnetic field. In this sense, magnetic effects could be much stronger than in real life, if it weren’t for the fact that ferromagnets, all having the same chirality, can’t interact directly with each other. That’s not to say they can’t interact at all though. The field produced by one ferromagnet could be reflected from a diamagnet or paramagnet of the orbital type, changing its chirality in the process, then that field could interact with another ferromagnet. Ferromagnetic materials also exhibit diamagnetism too, so they can interact in this way.
It’s not entirely obvious whether the increase in magnetic effects due to ferromagnets not forming domains or the decrease due to ferromagnets not directly interacting would tend to win out overall, and there are of course the details of individual chemicals to consider, but there are at least intriguing possibilities.
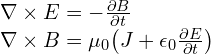
Leave a Reply