Schrödinger’s equation generalises very naturally to 4D, but there are a few details that are a bit more tricky to derive. The number of spin states, the magnetic moment, and in general the behaviour of relativistic electrons, is not quite so obvious. It would be easy to just assume that, like in real life, there are 2 spin states, but then the magnetic moment and spin-orbit coupling associated with them isn’t so obvious. In order to resolve these questions, I will be taking a brief detour to the most fundamental level of physics that’s currently understood, quantum field theory.
This post will be considerably more technical than most of the rest, and assume a higher level of understanding of quantum mechanics. It is safe to skip it, as the results that are needed are much simpler than the methods used to derive them. I will not be attempting to give a full explanation of QFT, since that would take far too long, but I can recommend this as a relatively brief and clear introduction to the subject. There are still a lot of technicalities I’ll be skipping over even in the areas I do cover, such as the differences between representations of a Lie group, its universal cover and its Lie algebra.
Each particle in a field theory has an associated field, whose values at each point in space are elements of a projective representation of the Lorentz group ![]() (with the caveat that it’s more like a joint probability distribution of values rather than the fields having definite values, since this is quantum mechanics). The spin of an electron, i.e. which representation it has, is a key part of what makes it an electron, but the representations of
(with the caveat that it’s more like a joint probability distribution of values rather than the fields having definite values, since this is quantum mechanics). The spin of an electron, i.e. which representation it has, is a key part of what makes it an electron, but the representations of ![]() that are relevant in real life are different from the representations of
that are relevant in real life are different from the representations of ![]() that would correspond to 4D particles, so the issue is to identify which representation to pick for the 4D electron and how that fits into an equivalent of the quantum electrodynamics Lagrangian.
that would correspond to 4D particles, so the issue is to identify which representation to pick for the 4D electron and how that fits into an equivalent of the quantum electrodynamics Lagrangian.
The QED Lagrangian density is
![]()
where the electromagnetic field ![]() , the photon field is
, the photon field is ![]() , the electron field
, the electron field ![]() is a complex bispinor and
is a complex bispinor and ![]() . The photon field must have vector values in order for the sum
. The photon field must have vector values in order for the sum ![]() to make sense, and the vector representation exists in all dimensions since it is the defining feature of
to make sense, and the vector representation exists in all dimensions since it is the defining feature of ![]() .
.
To make the significance of the bispinor field clearer, it will help to rearrange the Lagrangian a bit to emphasise the role of the representations. Every pair of representations, ![]() of the same group has a product
of the same group has a product ![]() , and like all finite-dimensional representations (of sufficiently well-behaved groups), it can be decomposed as a sum of irreducible representations. Projecting the product onto one of these irreducible representations gives a way of multiplying elements of
, and like all finite-dimensional representations (of sufficiently well-behaved groups), it can be decomposed as a sum of irreducible representations. Projecting the product onto one of these irreducible representations gives a way of multiplying elements of ![]() and
and ![]() , and by the universal property of the tensor product and direct sum, all polynomial expressions in elements of these representations can be expressed as combinations of these products.
, and by the universal property of the tensor product and direct sum, all polynomial expressions in elements of these representations can be expressed as combinations of these products.
As an example, consider the vector representation of ![]() . For now, let’s label each representation by its dimension (since those uniquely identify projective representations of
. For now, let’s label each representation by its dimension (since those uniquely identify projective representations of ![]() ), then the vector representation is labelled
), then the vector representation is labelled ![]() , and we have the equation
, and we have the equation ![]() , which means that two vectors can be multiplied together to give a scalar (1), another vector (3) or a trace-free symmetric rank-2 tensor. The first two of these are (up to an arbitrary scale factor) simply the usual dot product and cross product. For this reason, whenever there is a scalar resp. vector product available between two representations, I will be using the notation
, which means that two vectors can be multiplied together to give a scalar (1), another vector (3) or a trace-free symmetric rank-2 tensor. The first two of these are (up to an arbitrary scale factor) simply the usual dot product and cross product. For this reason, whenever there is a scalar resp. vector product available between two representations, I will be using the notation ![]() resp.
resp. ![]() for it.
for it.
The irreducible representations of ![]() can be identified by their dimension, but it is more conventional to label them by their spins,
can be identified by their dimension, but it is more conventional to label them by their spins, ![]() for scalar,
for scalar, ![]() for spinor,
for spinor, ![]() for vector and so on. The complexification of
for vector and so on. The complexification of ![]() is equal to the complexification of
is equal to the complexification of ![]() , so any complex representation of
, so any complex representation of ![]() can be labelled by the spins of its left- and right-chiral parts, in the form
can be labelled by the spins of its left- and right-chiral parts, in the form ![]() . In this format, the vector representation is
. In this format, the vector representation is ![]() , the scalar is
, the scalar is ![]() and the bispinor is
and the bispinor is ![]() . The available products between two bispinors are two scalars (one chiral and one not, we’ll be using the achiral one), two vectors (one symmetric and one antisymmetric, we’ll be using the symmetric one) and some irrelevant higher-spin components. Using this notation, the Lagrangian density can be expressed as
. The available products between two bispinors are two scalars (one chiral and one not, we’ll be using the achiral one), two vectors (one symmetric and one antisymmetric, we’ll be using the symmetric one) and some irrelevant higher-spin components. Using this notation, the Lagrangian density can be expressed as
![]()
The representations of ![]() are of course a bit more complicated than for
are of course a bit more complicated than for ![]() . Since
. Since ![]() , any representation of
, any representation of ![]() is also a representation of
is also a representation of ![]() , and the irreducible representations of
, and the irreducible representations of ![]() can be expressed as direct sums of the irreducible representations of
can be expressed as direct sums of the irreducible representations of ![]() which, as mentioned earlier, can be described by their left-chiral spin and their right-chiral spin. If we arrange the irreducible representations of
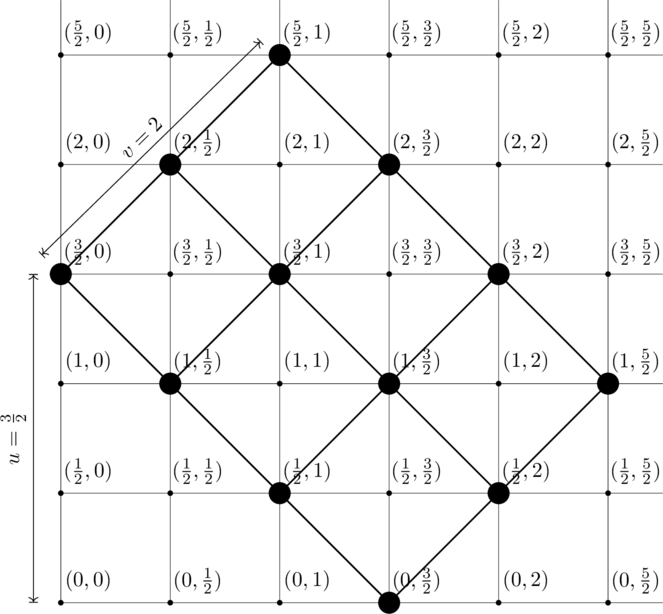
which, as mentioned earlier, can be described by their left-chiral spin and their right-chiral spin. If we arrange the irreducible representations of ![]() in a grid as shown
in a grid as shown
then the complex irreducible representations of ![]() are the direct sum of a set of these that form a diagonal rectangle contacting both axes:
are the direct sum of a set of these that form a diagonal rectangle contacting both axes:
The thick lines represent the action of the boosts, the elements of ![]() that mix the time and space coordinates. These representations can be identified by 2 numbers, as shown on the diagram. They are denoted
that mix the time and space coordinates. These representations can be identified by 2 numbers, as shown on the diagram. They are denoted ![]() . In this notation, the scalar is
. In this notation, the scalar is ![]() , the vector is
, the vector is ![]() and the spinor is
and the spinor is ![]() . I’m not entirely sure my derivation for this structure is correct, but for these specific low-spin representations at least I’m more confident. Representations with
. I’m not entirely sure my derivation for this structure is correct, but for these specific low-spin representations at least I’m more confident. Representations with ![]() have the odd property that at low energies they act like there are multiple different spins possible. I’m not really sure how to interpret this, but perhaps they would require some analogue of gauge fixing like massless spin-1 fields in 3D space do, which raises the odd possibility of gauge fermions.
have the odd property that at low energies they act like there are multiple different spins possible. I’m not really sure how to interpret this, but perhaps they would require some analogue of gauge fixing like massless spin-1 fields in 3D space do, which raises the odd possibility of gauge fermions.
I identify ![]() as the equivalent of the bispinor representation in 3D space for several reasons. It is the only representation which is entirely spin-
as the equivalent of the bispinor representation in 3D space for several reasons. It is the only representation which is entirely spin-![]() . Its products with itself, the irreducible components of
. Its products with itself, the irreducible components of ![]() , are
, are ![]() ,
, ![]() , and
, and ![]() , the scalar, vector and bivector representations, which gives us everything we need for the QED Lagrangian. Finally, of course there’s also the fact that the equations of motion turn out to be similar to Dirac’s equation. This last part on its own would be sufficient to make the choice of course, but the others suggest the choice is unique.
, the scalar, vector and bivector representations, which gives us everything we need for the QED Lagrangian. Finally, of course there’s also the fact that the equations of motion turn out to be similar to Dirac’s equation. This last part on its own would be sufficient to make the choice of course, but the others suggest the choice is unique.
With the electron field ![]() taking values in
taking values in ![]() and the photon field
and the photon field ![]() taking 5-vector values (i.e. space-time vectors where space is 4D), the Lagrangian density for the 4D equivalent of QED is then
taking 5-vector values (i.e. space-time vectors where space is 4D), the Lagrangian density for the 4D equivalent of QED is then
that is, exactly the same as in the real-world case given the notation. There is again a choice of which products to use. As a complex representation, ![]() has only one scalar part and one vector part, but the product of the real versions,
has only one scalar part and one vector part, but the product of the real versions, ![]() has 4 real scalar parts and 4 real vector parts. Although it’s often written as a complex number, the Lagrangian is actually real, and any of these products could appear in the Lagrangian for a general particle, but in order for charge conservation to work, complex linearity is necessary, and there’s only one version of each product that’s complex linear. There is a choice of overall scale factor for each, but they are of no physical consequence since the fields and the parameter
has 4 real scalar parts and 4 real vector parts. Although it’s often written as a complex number, the Lagrangian is actually real, and any of these products could appear in the Lagrangian for a general particle, but in order for charge conservation to work, complex linearity is necessary, and there’s only one version of each product that’s complex linear. There is a choice of overall scale factor for each, but they are of no physical consequence since the fields and the parameter ![]() can be scaled to compensate for any changes (except changes of sign, in which case I’ll be going with the one that works out right in the end).
can be scaled to compensate for any changes (except changes of sign, in which case I’ll be going with the one that works out right in the end).
Filling in the explicit formulas for the products, we can convert this Lagrangian back into a form with indices and gamma matrices. Again, the formula looks exactly the same
only the definition of the gamma matrices changes. The derivation of the gamma matrices is rather tedious and I’ll spare you the details, but the result is
These are, unsurprisingly, just the usual gamma matrices with the addition of ![]() as
as ![]() . It would not have been hard to guess that this would be the result, but it’s nice to see that it worked out starting from the representation theory.
. It would not have been hard to guess that this would be the result, but it’s nice to see that it worked out starting from the representation theory.
Since the Lagrangian has the same form, the derivation of Dirac’s equation follows the same path as usual and arrives at the same result,
where again the set of gamma matrices just has an extra element added.
Considering plane wave solutions with zero momentum, i.e. ![]() , this reduces to
, this reduces to ![]() . This eigenvalue equation has solutions
. This eigenvalue equation has solutions ![]() , where
, where ![]() has its first 2 or last 2 components equal to
has its first 2 or last 2 components equal to ![]() depending on the sign of
depending on the sign of ![]() , which shows that at low energies these components of
, which shows that at low energies these components of ![]() correspond to the particle and the antiparticle. Each pair of components transforms under a different chiral representation of
correspond to the particle and the antiparticle. Each pair of components transforms under a different chiral representation of ![]() , either
, either ![]() or
or ![]() , which implies that the electron and the positron are chiral and have opposite chiralities.
, which implies that the electron and the positron are chiral and have opposite chiralities.
To see this more explicitly, let’s solve approximately for a single one of these pairs in the case where the momentum is much less than the energy. Let
![Rendered by QuickLaTeX.com \[\psi = \left [ \begin{array}{c} \psi_{+} \\ \psi_{-} \end{array} \right ] \]](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-666192eed7fb349940e3f38bf4af2803_l3.png)
so that each of ![]() and
and ![]() has 2 components. First we expand Dirac’s equation in these components (while re-introducing the constant
has 2 components. First we expand Dirac’s equation in these components (while re-introducing the constant ![]() explicitly, which had previously been set to
explicitly, which had previously been set to ![]() and ignored):
and ignored):
If we assume this is a low-energy state containing an electron rather than a positron, the first term in the equation, for ![]() ,
, ![]() is much larger than the other terms because it involves the time derivative therefore
is much larger than the other terms because it involves the time derivative therefore ![]() . Again using the assumption that this is an electron not a positron,
. Again using the assumption that this is an electron not a positron, ![]() is much smaller than
is much smaller than ![]() and its dynamics is mostly driven by
and its dynamics is mostly driven by ![]() rather than having its own thing going on. Treating the
rather than having its own thing going on. Treating the ![]() terms as a simply oscillating value
terms as a simply oscillating value ![]() , the rest of the equation
, the rest of the equation ![]() can be rearranged to
can be rearranged to ![]() which oscillates around
which oscillates around ![]() . The oscillations are the positronic part we’re avoiding, so if we just use this as the value of
. The oscillations are the positronic part we’re avoiding, so if we just use this as the value of ![]() ,
,
Substituting this into the equation for ![]() , and defining the electric and magnetic fields
, and defining the electric and magnetic fields ![]() and
and ![]() and time derivative
and time derivative ![]() we get
we get
(where ![]() includes only the spatial components). The magnetic terms at the end show the chiral nature of the 4D electron particularly clearly. The magnetic field is a bivector, just like in 3D space, but unlike the 3D case, bivectors in 4D are not equivalent to vectors. There are six components of the magnetic field,
includes only the spatial components). The magnetic terms at the end show the chiral nature of the 4D electron particularly clearly. The magnetic field is a bivector, just like in 3D space, but unlike the 3D case, bivectors in 4D are not equivalent to vectors. There are six components of the magnetic field, ![]() , which can be organised into two groups of three with opposite chiralities,
, which can be organised into two groups of three with opposite chiralities,
The electron’s inherent magnetic moment only interacts with one of these sets, and the positron’s only with the other. It would be possible to derive the magnetic field the electron produces more formally by varying the photon field instead of the electron field and deriving its equations of motion, but a simpler argument based on the conservation of energy implies that the magnetic field produced by the electron is chiral in the opposite way to the field it reacts to.
The spin-orbit coupling also exhibits this chiral effect, which I expect to lead to a slight splitting of the energies of certain d orbitals and minor differences between enantiomers, but in cases where relativistic effects are not relevant and additionally there is no magnetic field, the equation above reduces to
i.e. Schrödinger’s equation (with the mass-energy included), which is not chiral, therefore the effects of the electron’s chirality on chemistry are expected to be small in most cases.
At this point I’ve demonstrated all of what I need to move on to the actual chemistry, but there is another minor oddity to note. Recall the QED Lagrangian
Suppose we change the coordinate system by scaling all the axes by some factor ![]() . Then the derivatives scale like
. Then the derivatives scale like ![]() and in order for the overall action, which is a 5 dimensional integral over the Lagrangian density, to remain constant, the Lagrangian density as a whole must scale as
and in order for the overall action, which is a 5 dimensional integral over the Lagrangian density, to remain constant, the Lagrangian density as a whole must scale as ![]() . The photon kinetic term is order 2 in
. The photon kinetic term is order 2 in ![]() and order 2 in
and order 2 in ![]() , therefore
, therefore ![]() must scale like
must scale like ![]() . Similarly,
. Similarly, ![]() must scale as
must scale as ![]() because of its kinetic term. The photon-electron coupling term is order 2 in
because of its kinetic term. The photon-electron coupling term is order 2 in ![]() , 1 in
, 1 in ![]() and 1 in
and 1 in ![]() therefore
therefore ![]() scales like
scales like ![]() . In 3D,
. In 3D, ![]() does not scale at all, which makes QED renormalizable, but in 4D, the coupling appears to get stronger as we zoom in, making (at least this version of) QED in 4D non-renormalizable. This implies that it can’t be used to predict high-energy behaviour or calculate highly precise corrections to the electron’s low-energy properties like it can in real life, but I wasn’t planning on doing those calculations anyway. It may not be a fully consistent theory as stated, but consistent non-renormalizable theories evidently can exist given that gravity physically does exist, even if we don’t know at the moment how to fully explain it.
does not scale at all, which makes QED renormalizable, but in 4D, the coupling appears to get stronger as we zoom in, making (at least this version of) QED in 4D non-renormalizable. This implies that it can’t be used to predict high-energy behaviour or calculate highly precise corrections to the electron’s low-energy properties like it can in real life, but I wasn’t planning on doing those calculations anyway. It may not be a fully consistent theory as stated, but consistent non-renormalizable theories evidently can exist given that gravity physically does exist, even if we don’t know at the moment how to fully explain it.

![Rendered by QuickLaTeX.com \begin{equations*} \gamma^0 = \left [ \begin{array}{cccc} 1 & & & \\ & 1 & & \\ & & -1 & \\ & & & -1 \\ \end{array} \right ] \quad \gamma^1 = \left [ \begin{array}{cccc} & & -1 & \\ & & & -1 \\ 1 & & & \\ & 1 & & \\ \end{array} \right ] \quad \gamma^2 = \left [ \begin{array}{cccc} & & -i & \\ & & & i \\ -i & & & \\ & i & & \\ \end{array} \right ] \\ \gamma^3 = \left [ \begin{array}{cccc} & & & -1 \\ & & 1 & \\ & -1 & & \\ 1 & & & \\ \end{array} \right ] \quad \gamma^4 = \left [ \begin{array}{cccc} & & & i \\ & & i & \\ & i & & \\ i & & & \\ \end{array} \right ] \end{equations*}](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-73511c8279c483f18b4c8759c24893bb_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} mc\psi_+ = & -(eA_0-i\partial_0)\psi_+ \\ + & (eA_1-i\partial_1)\left [ \begin{array}{cc} -1 & \\ & -1 \end{array} \right ] \psi_- \\ + & (eA_2-i\partial_2)\left [ \begin{array}{cc} -i & \\ & i \end{array} \right ] \psi_- \\ + & (eA_3-i\partial_3)\left [ \begin{array}{cc} & -1 \\ 1 & \end{array} \right ] \psi_- \\ + & (eA_4-i\partial_4)\left [ \begin{array}{cc} & i \\ i & \end{array} \right ] \psi_- \\ -mc\psi_- = & -(eA_0-i\partial_0)\psi_- \\ + & (eA_1-i\partial_1)\left [ \begin{array}{cc} -1 & \\ & -1 \end{array} \right ] \psi_+ \\ + & (eA_2-i\partial_2)\left [ \begin{array}{cc} i & \\ & -i \end{array} \right ] \psi_+ \\ + & (eA_3-i\partial_3)\left [ \begin{array}{cc} & 1 \\ -1 & \end{array} \right ] \psi_+ \\ + & (eA_4-i\partial_4)\left [ \begin{array}{cc} & -i \\ -i & \end{array} \right ] \psi_+ \end{align*}](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-48a0bff17b848eb8b55f4eb114da1ed9_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \psi_+ \approx & \frac 1 {2mc}\left( \\ & (eA_1-i\partial_1)\left [ \begin{array}{cc} -1 & \\ & -1 \end{array} \right ] \\ + & (eA_2-i\partial_2)\left [ \begin{array}{cc} -i & \\ & i \end{array} \right ] \\ + & (eA_3-i\partial_3)\left [ \begin{array}{cc} & -1 \\ 1 & \end{array} \right ] \\ + & (eA_4-i\partial_4)\left [ \begin{array}{cc} & i \\ i & \end{array} \right ] \\ & ) \psi_- \end{align*}](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-d733eb790709c5090af3248daa4f5f01_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} i \frac {\mathrm d} {\mathrm dt} \psi_- & \approx (mc^2 + ceA_0)\psi_- + \frac 1 {2m} \\ \big ( & (eA_1-i\partial_1)\left [ \begin{array}{cc} -1 & \\ & -1 \end{array} \right ] + (eA_2-i\partial_2)\left [ \begin{array}{cc} i & \\ & -i \end{array} \right ] \\ & \quad + (eA_3-i\partial_3)\left [ \begin{array}{cc} & 1 \\ -1 & \end{array} \right ] + (eA_4-i\partial_4)\left [ \begin{array}{cc} & -i \\ -i & \end{array} \right ] \big ) \\ \big ( & (eA_1-i\partial_1)\left [ \begin{array}{cc} -1 & \\ & -1 \end{array} \right ] + (eA_2-i\partial_2)\left [ \begin{array}{cc} -i & \\ & i \end{array} \right ] \\ & \quad + (eA_3-i\partial_3)\left [ \begin{array}{cc} & -1 \\ 1 & \end{array} \right ] + (eA_4-i\partial_4)\left [ \begin{array}{cc} & i \\ i & \end{array} \right ] \big ) \psi_- \end{align*}](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-ac052963a0baef86c42def3fa55967b8_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} i \frac {\mathrm d} {\mathrm dt} \psi_- & \approx (mc^2 + e\phi)\psi_- \\ + & \frac 1 {2m} \Big ( e^2 A^2 \psi_- -ie\nabla \cdot (A \psi_-) -ieA \cdot \nabla \psi_- - \nabla^2 \psi_- \\ & -ie \big( (B_{12} + B_{34}) \left [ \begin{array}{cc} i & \\ & -i \end{array} \right ] + (B_{13} + B_{42}) \left [ \begin{array}{cc} & 1 \\ -1 & \end{array} \right ] \\ & \qquad \qquad + (B_{14} + B_{23}) \left [ \begin{array}{cc} & -i \\ -i & \end{array} \right ] \big ) \psi_- \\ & \Big ) \end{align*}](https://blog.4denthusiast.net/wp-content/ql-cache/quicklatex.com-2984b97c6a349f8b9c00f875d9c19f38_l3.png)
Leave a Reply